コイルは、電流を磁気に換えて貯める入れ物です。コイルの容量は巻き線の回数に比例（同一コア上の巻き線なら二乗比例）して大きくなります。直列に接続する事は巻き数の増加になりませので、容量は加算されます。一方並列では巻き数の変化はないもののエネルギーが並列分、分散されますので、容量は減少します。
直列接続の計算：
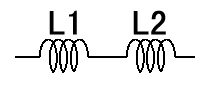単純に加算するだけです。１０μHと２２μＨを直列につなぐと３２μＨになります。
数式のすきな人には合成インダクタンスをＬ、接続するコイルをＬ１、Ｌ２とすると
Ｌ＝Ｌ１＋L２ になります。
並列接続の計算：
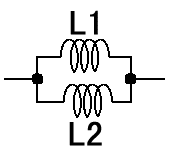単純にはいきません。いきなり数式のやっかいになります。合成インダクタンスをＬ、接続するコイルをＬ１、Ｌ２とすると
Ｌ＝１／(１／Ｌ１+１／Ｌ２)で計算できます。３本以上は（かっこ）の中がコイルの個数分増えます。式を横に書いたので判りにくいですが、個々のンダクタンス値を逆数にして、全て加算し、結果を再度逆数にしたのが並列インダクタンスの計算です。
コイルの並列計算に便利な式
２本の並列計算に限り、次の式が使えますＬ＝Ｌ１＊Ｌ２／（Ｌ１＋Ｌ２）
複雑そうですが２本の値を掛け算した数値を足し算した数値で割るだけです。
「和分の積」と憶えれば憶えやすいそうです。３本以上は２本の並列計算を繰り返す事で求められます。
 |
 |
 |