抵抗は、流れをじゃまする働きがあります。混雑した道路みたいなものと考えるとわかり易くなります。混雑した路は距離が長くなると通過に時間がかかります。逆に平行する路が多ければ通過しやすくなり、時間が短くなります。
抵抗で考えた場合、抵抗同士を直列につなぐ事はじゃまする部分が増える事に、並列につなぐ事は通過がしやすくなり、抵抗値が下がります。
直列接続の計算：
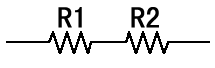単純に加算するだけです。１０ＫΩと２２ＫΩを直列につなぐと３２ＫΩになります。
数式のすきな人には合成抵抗をＲ、接続する抵抗をＲ１、Ｒ２とすると
Ｒ＝Ｒ１＋Ｒ２ になります。
並列接続の計算：
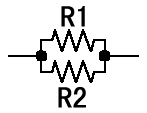単純にはいきません。いきなり数式のやっかいになります。合成抵抗をＲ、接続する抵抗をＲ１、Ｒ２とすると
Ｒ＝１／(１／Ｒ１+１／Ｒ２)で計算できます。３本以上は（かっこ）の中が抵抗の個数分増えます。式を横に書いたので判りにくいですが、個々の抵抗値を逆数にして、全て加算し、結果を再度逆数にしたのが並列抵抗の計算です。
式ではこうなるのですが、並列計算は抵抗を逆に考えて通しやすさに換算すればそのまま加算できる事意味しています。ちなみに抵抗の逆数も存在し、昔はΩの上下を反対にした記号を書き読み方もオーム（ＯＨＭ）を逆に読んだモー（ＭＨＯ）が使用されていました。最近は国際的にＳ（シーメンス）に統一されました。
抵抗の並列計算に便利な式
２本の並列計算に限り、次の式が使えますＲ＝Ｒ１＊Ｒ２／（Ｒ１＋Ｒ２）
複雑そうですが２本の値を掛け算した数値を足し算した数値で割るだけです。
「和分の積」と憶えれば憶えやすいそうです。３本以上は２本の並列計算を繰り返す事で求められます。
 |
 |
 |